Две недели назад, 15-ого декабря мы начали разговор о проектах на C/C++. В этой заметке я постараюсь изложить небольшой материал на этот и последующие семинары, который, хотя и не будет вполне повторять темы освещённые в устном изложении, содержит те нужные части семинара, которые студенты обычно записывают. Я хотел бы, чтобы на наших семинарах мы больше говорили и думали, и меньше писали. Только так на мой взгляд, получится познакомиться с этими техническими вещами достаточно бегло и быстро, чтобы к весне сделать первые виртуальные ядерно-физические установки в Geant4 с сопутствующей обработкой.

Эзотерика программирования

Для того чтобы приобрести очень важное в начале курса ощущение (get feeling) процесса разработки собственной программы, попробуем написать простейшее приложение самостоятельно. Именно ощущение процесса нам будет важно, поскольку в конечном итоге это единственное, что свидетельствует о правильности той последовательности прототипирования, которой вы будете придерживаться при самостоятельной работе в дальнейшем.

Оговорюсь, что хотя лично я и большинство программистов считает верным путём модели разработки при которых вы проектируете код прежде чем его писать, сам этот навык проектирования приходит с опытом, и его развитие не входит в программу наших семинаров, иначе бы пришлось делать их невообразимо долгими.

Я думаю, что вместо этого целесообразно начать с прототипно-ориентированного подхода предполагающего экстенсивную разработку. Выглядит это как последовательное наращивание функциональности программы, от базовых структурных элементов, очевидных в начале: так, например, если вы знаете, что у вас в программе будет какая-то математическая функция, алгоритм, функциональный элемент, вы реализуете этот отдельный блок кода, тестируете его небольшим фрагментом кода в точке входа, и переходите к следующему, может быть, менее очевидному. Размножая затем эти блоки, вы организуете частично работающий прототип, который в какой-то момент начинает приближаться по своему поведению к программе которую вы хотите получить и, в итоге, становится ей.

По мере того как вы будете переходить от вполне очевидных структурных и функциональных элементов к менее очевидным, вам сделаются видны скрытые взаимосвязи и сущности весьма абстрактной природы: обобщённые контейнеры, шаблоны проектирования, общие схемы взаимодействия и т.д. В какой-то момент, на десятом-двадцатом своём проекте вы, может быть, начнёте приобретать видение достаточное для первых попыток проектировать программу перед её написанием.

Но до тех пор целесообразно придерживаться подхода экстенсивного прототипирования. И многие опытные физики-счётчики, в принципе, никакой другой подход не эксплуатируют, годами работая в этой примитивной системе, стиле который я нызываю "стиль бродячего акына — что вижу, о том и пою". Хотя эта практика и весьма порочна в долгосрочной перспективе, её преимущества в начале пути мне кажутся бесспорными. Многие её особенности затем получают развитие: так, например, привычка тестировать небольшие блоки кода затем превращается в практику написания модулей тестов (unit test).

Программа-прототип генерирующая числа с заданной функцией плотности распределения

Итак, любая программа выполняющая симуляцию по методу Монте-Карло содержит в себе генератор чисел с заданной плотностью распределения. В простейшем случае, в случае однородной плотности распределения, это будет обычный random uniform присутствующий в любом языке программирования: обычно это функции с именами вроде rand(), randint(), random(), etc.

В более интересных для физика случаях требуется сгенерировать последовательность чисел с какой-то заданной плотностью. Вообще говоря, общеупотребимыми методами здесь являются:

1. Метод Неймана¹ ("обычный", "прямой", etc)
2. Метод обратной функции (inverse transform sampling, метод обратного преобразования, метод Смирнова)
3. Модифицированный метод Неймана

Наиболее вычислительно-эффективным и аналитически-строгим является метод обратной функции. Поговорим о нём позже, на семинарах, если будет запрос со стороны аудитории. По моим наблюдениям, при его изложении больше внимания приходится уделять математической стороне вопроса нежели программированию, так что это (безусловно важное) знание пока отложим. Важно, однако, отметить, что метод обратной функции сам по себе применим для функций плотности распределения допускающих определённое аналитическое представление их интегрального функционала, и из-за этого ограничения нередко оказывается бесполезен на практике per se.

Прямой метод Неймана прост как палка, несложен в реализации, очень иллюстративен, но не пригоден для практических приложений в большинстве случаев в виду его вычислительной дороговизны. Мы, тем не менее, реализуем его сейчас.

Модифицированный метод Неймана сочетает в себе прямой метод и метод обратной функции.

Прямой метод Неймана

Суть его для одномерной функции плотности состоит в одновременном разыгрывании пар независимых случайных чисел $x, y$ (нескоррелированных³), и проверке какого-нибудь одного числа на условие $y <= f(x)$. Визуально это соответствует тому как если бы вы ставили в произвольном месте точки на графике функции плотности распределения и отбирали только те, что попадают под (или на) кривую.

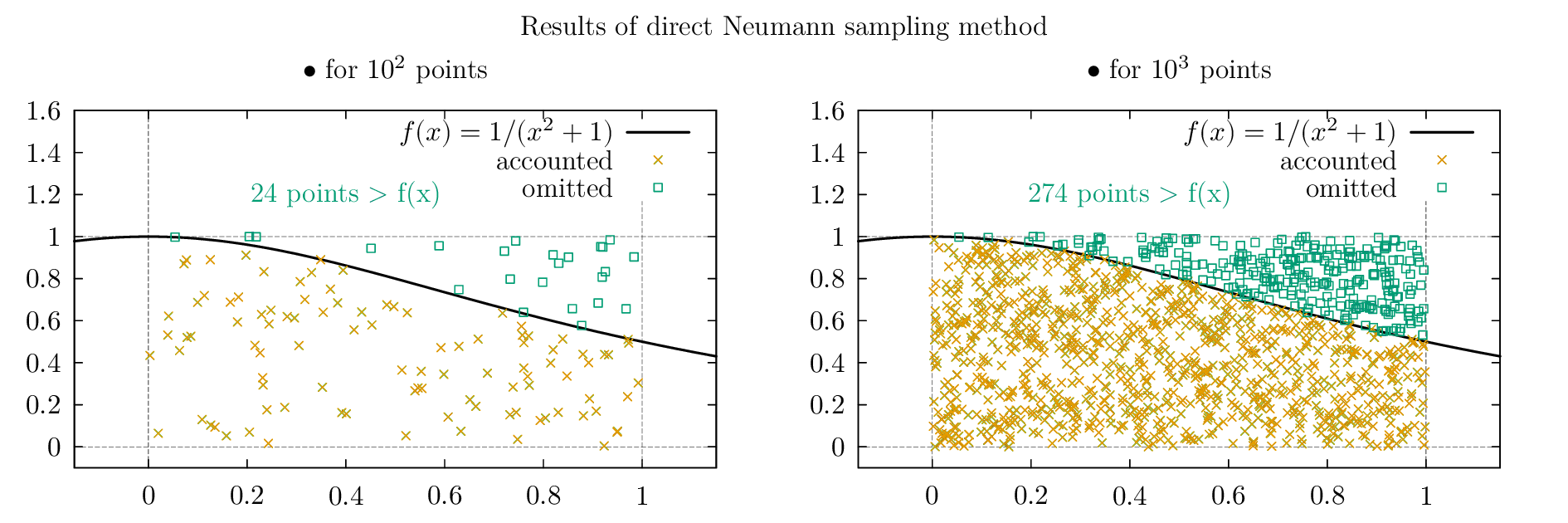
Для алгоритма входными параметрами будут служить:

• Функция плотности распределения случайной величины
• Область определения этой функции плотности распределения

Полезной, при реализации алгоритма, характеристикой, извлекаемой из этих входных параметров, будет максимальное значение функции плотности распределения на интервале её определения.

Возьмём в качестве примера функцию $f(x) = 1/(x^2 + 1)$. Чтобы сделать из неё функцию плотности распределения, нужно, понятно, отнормировать её в области определения (которую возьмём для простоты $[0..1]$). Нормировочная константа:

$$ C = \int\limits_0^1 \frac{1}{x^2 + 1} dx = \arctan(x) \bigg\rvert_0^1 = \pi/4 $$

Однако, беглое рассуждение о том как работает прямой метод Неймана говорит нам, что нормировка функции плотности распределения не должна никаким образом повлиять на характер генерируемой числовой последовательности. Нормировочная константа пригодится нам позже, для проверки наблюдаемого распределения против истинной функции плотности вероятности, которая будет выглядеть вот так:

$$ \frac{d p(x)}{d x} = \frac{ 4 }{\pi \cdot (x^2 + 1)} $$

Работать с $f(x)$ вместо $dp(x)/dx$ несколько проще ещё и тем что максимум этой функции приходится ровнёхонько на единицу, т.е. мы будем разыгрывать пары случайных чисел $ x, y \in [0..1] $.

Шаг первый: тестируем функцию

Очевидно, что в программе удобно выделить функцию плотности распределения как отдельную функцию (в терминах языка Си процедуры возвращающие значения называют функциями, однако поскольку функция имеет побочные эффекты, она чаще всего фактически является процедурой с возвращаемым значением; см. релевантный вопрос на SO).

Напишем небольшую программу для того чтобы протестировать работу целевой функции. Пусть это будет просто список значений функции в интервале 0. ... 0.9:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13

# include <stdio.h>

float _f(float x) {
    return 1/(x*x + 1);
}

int main(int argc, char * argv[]) {
    int i;
    for( i = 0; i < 10; i++ ) {
        printf( "%d %f\n", i, _f(.1*i) );
    }
    return 0;
}

Скомпилируем программу вручную и запустим:

$ g++ ./main.c
$ ./a.out

Программа напечатает номер и значение функции посредством printf() в десяти точках. В качестве небольшого упражнения попробуйте модифицировать вызов функции printf() так чтобы она печатала вам значение $x$ вместо номера точки.

Шаг второй: вызов random()

Посмотрим, в каком заголовочном файле стандартной библиотеки находится функция random() и убедимся, что она делает то что нам нужно на странице справки, которую можно посмотреть например через $ man random, попутно отметив, что результат вызова этой функции — длинное целое число в диапазоне 0..RAND_MAX (о том что такое RAND_MAX я уже сказал пару слов на семинаре):

$ man random
SYNOPSIS
       #include <stdlib.h>

       long int random(void);
       ...

Включим в программу заголовочный файл stdlib.h и изменим тело внутри счётчика так чтобы убедиться, что мы верно понимаем результат работы random():

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16

# include <stdio.h>
# include <stdlib.h>

float _f(float x) {
    return 1/(x*x + 1);
}

int main(int argc, char * argv[]) {
    int i;
    float a, b;
    for( i = 0; i < 10; i++ ) {
        a = random() / ( (float) RAND_MAX );
        printf( "%f\n", a );
    }
    return 0;
}

Замечу, что целью данного экзёрсиса является не знакомство с какой-то конкретной функцией (вы их будете видеть и использовать сотни и тысячи, нет никакой нужды их запоминать), а навык поиска и эксперимента с техническим средством в целом:

• Смотреть справку легко и полезно
• Сделать "тестовый стенд" для того чтобы убедиться в правильности своего понимания просто и ничего не стоит

Последнее — очень важно. Хотя вы едва ли получите дезориентирующее понимание (misleading) для столь тривиального примера, во многих случаях вы сможете избежать массы ошибок просто поиграв с функцией, алгоритмом или целой технологией.

Шаг третий: генерация нескоррелированных пар и сравнение

Небольшое архитектурное соображение, которое сложно уловить на учебном примере, но всё же, вероятно, стоящее внимания: по мере того как ваша программа будет развиваться и усложняться, вам понадобится:

• Видеть структуру кода²
• Иметь возможность вызывать один и тот же блок в нескольких местах

Мы могли бы поместить блок генерации пары значений и сравнения внутрь цикла for() в функции main(), однако простейшее соображение, что в реальности вы едва ли будете пользоваться приложением которое просто печатает числа в стандартный поток вывода, но вероятнее всего будете вызывать функцию разыгрывающую случайную величину, наталкивает на мысль, что неплохо было бы выделить разыгрывание в отдельный смысловой блок, в отдельную функцию, которую вы могли бы вызывать в каких-то иных местах в программе. Назовём её roll(), и проверим, что она действительно способна выдавать число:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

# include <stdio.h>
# include <stdlib.h>

float _f(float x) {
    return 1/(x*x + 1);
}

float roll() {
    float a,b;
    do {
        a = random()/( (float) RAND_MAX );
        b = random()/( (float) RAND_MAX );
    } while( a > _f(b));
    return b;
}

int main(int argc, char * argv[]) {
    int i;
    float value;
    for( i = 0; i < 10; i++ ) {
        value = roll();
        printf("%f\n", value);
    }
    return 0;
}

Результатом работы такой программы будут десять чисел, которые, наверное, распределены так как нам нужно, но проверить это по десятку значений довольно затруднительно.

Шаг четвёртый — гистограмма

Не уверен, сколь плотно вы уже имели дела с гистограммами, но на всякий случай должен предупредить, что гистограммы — это краеугольный камень представления результатов измерений, да и вообще любой статистики. Это не просто один из существующих способов представления, это важнейший инструмент наглядной визуализации распределения случайной величины, по единственному взгляду на который человек часто способен сказать намного больше чем по набору чисел или таблице.

Помимо графического изображения гистограммы в виде столбцов, следует подумать о ней как об определённой структуре данных: в случае одномерной гистограммы, это будет просто упорядоченный конечный набор чисел — число отсчётов соответствующих определённому интервалу (из англоязычной номенклатуры пришёл термин "бин" — bin). Мы выберем равномерный биннинг гистограммы разбив область определения на десять равных бинов (каждый шириной $0.1$): $\{a_1 \rightarrow [0 .. 0.1); a_2 \rightarrow [0.1 .. 0.2) ... a_{10} \rightarrow [0.9 .. 1]\}$. Структура данных, таким образом, может быть легко описана массивом из десяти чисел, а само равномерное разбиение переводится в индекс массива простым машинным округлением случайной величины умноженной на $10$.

Машинное округление от математического отлично тем что не учитывает числа после запятой: отбрасываются все разряды (мантисса числа). Так, машинное округление приведёт $1.6$ к $1$ вместо двойки получающейся при математическом округлении.

Модифицируем теперь программу следующим образом:

• Объявим массив из десяти элементов-целых чисел counts
• Явно обнулим массив (это очень важно! подробнее расскажу на семинаре) функцией bzero() из заголовочного файла strings.h
• Будем увеличивать элемент массива counts соответствующий по номеру (индексу) машинному округлению случайной величины умноженной на $10$.
• После того как разыграем $n$ событий ($n$, кстати, запишем в специальную константу для красоты), напечатаем число отсчётов в каждом бине делённое на $n$ напротив значения функций $f(x)$.

Правильно предусмотрев все приведения типов, получим что-то вроде:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

# include <stdio.h>
# include <stdlib.h>
# include <strings.h>

float _f(float x) {
    return 1/(x*x + 1);
}

float roll() {
    float a,b;
    do {
        a = random()/( (float) RAND_MAX );
        b = random()/( (float) RAND_MAX );
    } while( a > _f(b));
    return b;
}

int main(int argc, char * argv[]) {
    int i;
    float value;
    int counts[10];
    const int n = 1e5;
    const int nBins = sizeof(counts)/sizeof(int);
    bzero( counts, sizeof(counts) );
    for( i = 0; i < n; i++ ) {
        value = roll();
        counts[(int) (value*10)] ++;
    }
    for( i = 0; i < nBins; ++i ) {
        printf( "%f %f\n", counts[i]/((float) n), _f( i/((float) nBins) ) );
    }
    return 0;
}

Понятно, что получившиеся два столбца позволяют нам оценить только форму распределения. Для полного сравнения, нам понадобится отнормированная $f(x)$, соответствующая, собственно, функции плотности распределения.

Шаг пятый: сравнение и базовое взаимодействие с пользователем

В качестве технических улучшений, для наглядного представления результатов теперь нанесём последние на сегодня штрихи:

• Изменим программу таким образом, чтобы считать относительную разницу: $|p(x) - \widetilde{p}(x)|/(p(x) + \widetilde{p}(x))$, где $p(x)$ — истинное значение плотности вероятности в точке соответствующей центру бина ($x_i+0.5$), а $\widetilde{p}(x)$ — разыгранное.
• Запишем для удобства чтения "измеренные" и истинные значения плотности вероятности в переменные, соответственно, ddp и dp, и напечатаем разницу в третьей колонке.

Теперь стратегически-важный момент: хотя вывод из такой программы, с учётом технических изменений, и отражает общую картину, практическая работа с ней неудобна для беглых экспериментов, поскольку не предусматривает удобных средств параметризации. Функциональное предназначение этого кода, хотя и апеллирует во многом к чисто академическим упражнениям, сущностно состоит в том чтобы продемонстрировать работоспособность прямого метода Неймана. Для этого мы, как минимум, должны предоставить возможность покатать апликуху на разном числе событий. Тут можно было бы лезть всякий раз в код программы, менять значение переменной n, собирать код и запускать её, однако есть более короткий (и как это будет в какой-то момент очевидно, чрезвычайно гибкий) способ сообщать приложениям простейшие параметры вроде чисел, коротких текстовых литералов или логических флагов: интерфейс командной строки.

О нём самом в деталях мы побеседуем ещё не раз на семинарах, однако вкратце: всё что вы напечатаете приложению из командной строки после имени исполняемого файла, будет помещено в массив строковых значений argv, при этом его первый (с индексом 0 в Си) элемент будет содержать имя приложения, а число элементов в массиве будет записано в переменную argc.

При этом понятно, что число введённое в консоли как, скажем, 42 будет строковой константой — то есть массивом из двух символов (char) 4 и 2, но не числом типа int. Для преобразования строки в число воспользуемся функцией atoi(), предполагая что число событий для генерации сообщено в первом аргументе командной строки (следующий после имени исполняемого файла токен отданный в командной строке при вызове).

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37

# include <stdio.h>
# include <stdlib.h>
# include <strings.h>
# include <math.h>

float _f(float x) {
    return 1/(x*x + 1);
}

float roll() {
    float a,b;
    do {
        a = random()/( (float) RAND_MAX );
        b = random()/( (float) RAND_MAX );
    } while( a > _f(b));
    return b;
}

int main(int argc, char * argv[]) {
    int i;
    float value, dp, ddp, delta;
    int counts[10];
    const int n = atoi(argv[1]);
    const int nBins = sizeof(counts)/sizeof(int);
    bzero( counts, sizeof(counts) );
    for( i = 0; i < n; i++ ) {
        value = roll();
        counts[(int) (value*10)] ++;
    }
    for( i = 0; i < nBins; ++i ) {
        ddp = counts[i]/((float) n);
        dp = _f((i+.5)/((float) nBins)) / (10*M_PI/4);
        delta = fabs(dp - ddp)/(dp + ddp);
        printf( "%f %f %e\n", dp, ddp, delta );
    }
    return 0;
}

Теперь после компиляции программы, вам следует вызывать её, например, следующим образом:

$ ./a.out 10

или

$ ./a.out 5000

Если вызвать исполняемый файл без этого аргумента, в лучшем случае (и чаще всего) процесс завершится с ошибкой сегментации. О том что это такое и её причинах поговорим на семинаре — после знакомства с указателями.

Заметим тут, что мы вычисляем интеграл плотности вероятности в бине довольно неточно, но для столь гладкой функции это не очевидно. Можете затеять детальный экзёрсис, это будет полезным мотивом чтобы разобраться в коде.

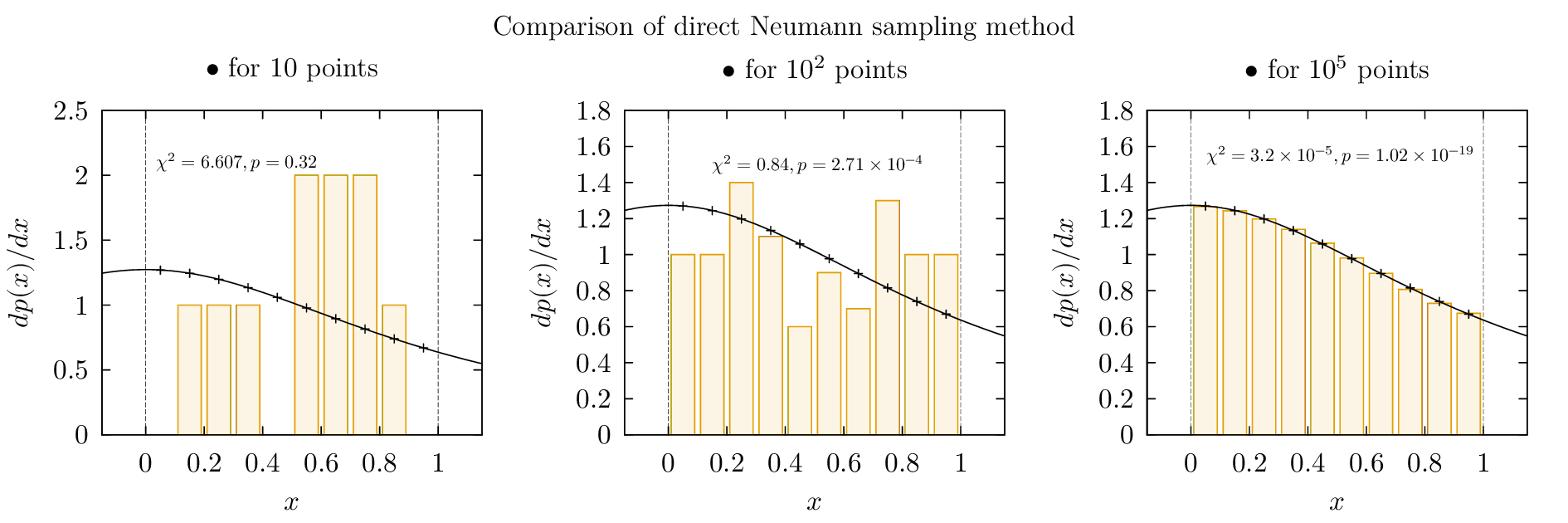
На графиках выше я попытался посчитать $\chi^2$-критерий для полученных выборок. Вам может быть интересно подумать над тем, как следует модифицировать программу для подобных вычислений — различные критерии согласия являются краеугольным камнем всякой экспериментальной науки. Вычисление p-value выполнено функцией gsl_cdf_chisq_P() библиотеки GSL, все графики построены в gnuplot. Исходные коды вы можете найти в нашем публичном репозитории кодов посвящённых этому и релевантным курсам.

Вопросы на следующий семинар

Мы бегло затронули несколько малознакомых тем в этом упражнении:

• Массивы, их размер, размер типов данных и оператор sizeof()
• Препроцессор языка Си: директивы #inlude и макросы RAND_INT, M_PI.
• Приведение типов в стиле Си: (int) v, (float) RAND_MAX, etc.
• Инициализация переменных и массивов; обнуление массива через bzero()
• Ошибка сегментации и аварийное завершение процессов в Linux

Я намеренно не касался их, потому что каждая из них в лучшем случае займёт минут пятнадцать устного изложения, в то время как записывать их здесь заслуживало бы отдельного поста.

Примечания

¹) Здесь я должен признать, что не встречал в литературе таких названий, и терминология эта в известной степени обиходная, взятая из профессионального слэнга. Всё что мне попадалось в монографиях — обычно оба метода названных здесь "прямым" и "модифицированным" излагаются как один общий "метод Неймана", а "метод обратной функции" оказывается органически включён в этот раздел. Тем не менее, с инженерной точки зрения целесообразно разделять эти метода в виду их различной алгоритмической сложности.

²) Здесь под структурой обычно понимается смысловая семантика процедур, циклов, тел выражений включённых в конструкции ветвления. Тело каждой из них увеличивает отбивку на фиксированное число пробелов (или табуляций).

³) Хотя отсутствие корреляции не гарантирует статистической независимости между числами пары, полезно сделать акцент лишь на её отсутствии, чтобы не рассматривать добротность генератора псевдослучайных чисел используемого функцией random() — подобное оказалось было бы далеко за рамками нашего курса.